Thuật giải Vương Hạo
B1: Phát biểu lại giả thiết và kết luận của vấn đề theo dạng chuẩn sau : GT1, GT2, ..., GTn KL1, KL2, ..., KLm
Trong đó các GTi và KLi là các mệnh đề được xây dựng từ các biến mệnh đề và 3 phép nối cơ bản : ∧ (dấu tuyển), ∨ (dấu hội) , ¬ (dấu bù)
| Phủ định của phủ định | ¬ (¬ p) ≡ p |
|---|---|
| (p ∨ q) ≡ (¬ p → q) | |
| Tương phản | (p → q) ≡ (¬ p → ¬ q) |
| De Morgan | ¬ (p ∨ q) ≡ (¬ p ∧ ¬ q) |
| ¬ (p ∧ q) ≡ (¬ p ∨ ¬ q) | |
| Giao hoán | (p ∧ q) ≡ (q ∧ p) |
| (p ∨ q) ≡ (q ∨ p) | |
| Kết hợp | (p ∧ q) ∧ r ≡ (p ∧ (q ∧ r)) |
| (p ∨ q) ∨ r ≡ (p ∨ (q ∨ r)) | |
| Phân phối | p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r ) |
| p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r ) |
B2 (Khử dấu ¬) Chuyển vế các GTi và KLi có dạng phủ định.
Ví dụ : p ∨ q, ¬(r ∧ s), ¬g, p ∨ r → s, ¬p
p ∨ q, p ∨ r, p → (r ∧ s), g, s
B3 (Khử dấu ∧, ∨): Nếu GTi có phép ∧, KLi có phép ∨ thì thay thế bằng dấu ","
Ví dụ : p ∧ q, r ∧ (¬p ∨ s) → ¬q, ¬s
p, q, r, ¬p ∨ s → ¬q, ¬s
B4 : Nếu GTi có phép ∨ hay ở KLi có phép ∧ thì tách thành hai dòng con.
| Ví dụ : p, ¬p ∨ q → q<=> | p, ¬p →q |
| p, q →q |
B5 : Một dòng được chứng minh nếu tồn tại chung một mệnh đề ở ở cả hai phía.
Ví dụ : p, q → q được chứng minh
p, ¬p → q <=> p → p, q
B6 :
a) Nếu một dòng không còn phép nối ∨ hoặc ∧ ở cả hai vế và ở 2 vế không có chung một biến mệnh đề thì dòng đó không được chứng minh.
b) Một vấn đề được chứng minh nếu tất cả dòng dẫn xuất từ dạng chuẩn ban đầu đều được chứng minh.


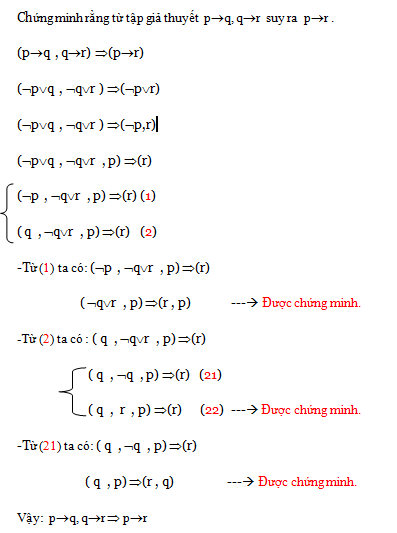


No comments: